I have been reading some of the entries on UCAR website about WRF performance and scaling, but I am confused about one thing: how are nested domains divided up between processors when running WRF that was compiled with dmpar options? I see from here that the x and y dimensions to the domain are divided by the factors of the number of cores. Does that apply to nested domains as well? What is the performance hit of adding a domain the same grid size with a grid ratio and time-step factor of 5?
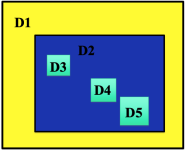
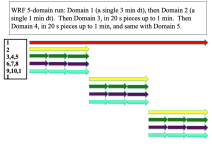
The reason I am asking I am trying to find the hypothetical time it would have taken my simulation to run on a different machine. I ran a 18 hr simulation with time step of 40 seconds, 5 total domains, each nested with grid ratio and time step factor of 5. The grid sizes were 102x102 for the course and 106x106 for all the fine domains. I assume this means that ~7.81 million grid points are integrated at each time step, but I could be off. I ran with 32 cores (Intel Xeon Processor E5-2670, 2.60 GHz) in dmpar config and it took 31 hours to complete.
Given what I read online, I can't get the math to work out to get even the same order of magnitude for the running time. If the parallel run divides the domain in to 26x13 or 27x14 subdomains, are all the nested domains divided similarly, so each subdomain is still roughly 5 times as expensive as it's parent? For my example this would mean we are computing 286,171 grid points per processor per timestep, or 463 million grid points over the course of the simulation.
Additionally, how many floating point or equivalent operations per grid cell are needed to integrate at each timestep? If I had a rough number I could more easily translate the runtime between machines. Assuming the domain breakdown I mentioned above and a rough processor performance of 5 Gflops, that comes out to 1.2 million floating point ops per grid point. Does that sound like the right ballpark?
My apologies in advance if I have misunderstood something fundamental. I'm an undergraduate who is completely new to NWP and only recently began using WRF.
The reason I am asking I am trying to find the hypothetical time it would have taken my simulation to run on a different machine. I ran a 18 hr simulation with time step of 40 seconds, 5 total domains, each nested with grid ratio and time step factor of 5. The grid sizes were 102x102 for the course and 106x106 for all the fine domains. I assume this means that ~7.81 million grid points are integrated at each time step, but I could be off. I ran with 32 cores (Intel Xeon Processor E5-2670, 2.60 GHz) in dmpar config and it took 31 hours to complete.
Given what I read online, I can't get the math to work out to get even the same order of magnitude for the running time. If the parallel run divides the domain in to 26x13 or 27x14 subdomains, are all the nested domains divided similarly, so each subdomain is still roughly 5 times as expensive as it's parent? For my example this would mean we are computing 286,171 grid points per processor per timestep, or 463 million grid points over the course of the simulation.
Additionally, how many floating point or equivalent operations per grid cell are needed to integrate at each timestep? If I had a rough number I could more easily translate the runtime between machines. Assuming the domain breakdown I mentioned above and a rough processor performance of 5 Gflops, that comes out to 1.2 million floating point ops per grid point. Does that sound like the right ballpark?
My apologies in advance if I have misunderstood something fundamental. I'm an undergraduate who is completely new to NWP and only recently began using WRF.