em_hill2d_x - solution only stable when dampening layer starts at z=5 km

[johanneshorak]

em_hill2d_x - solution only stable when dampening layer starts at 5km

Hi all! This is the second question I have with regards to the idealized simulations I've been running (other thread here: https://forum.mmm.ucar.edu/phpBB3/viewtopic.php?f=46&t=8463 )

With the setup I use, I only find stable solutions (or at least something close too it, see the problem in the other thread) for the model top set at 25km, a dampening layer with 20 km thickness and a dampening coefficient of 0.1. The problem is that I would rather not dampen far into the part of the atmosphere that's relevant for my studies. Ideally I'd have an undampened field up to 15km, so the dampening layer should not start below that.

I've tested the parameter space quite extensively so far. Even setting the model top 5km higher and keeping everything else the same didn't result in the analytical queney solution. I've scanned through about 2000 combinations of these values but to no avail. The only setting that seems to be working is the one mentioned above.

The question therefore is rather general - how can I get this to work? And why does it seem necessary to start dampening that low already?

I've run the simulations with em_hill2d_x with a sounding derived from:
U = 20 m/s (constant with height)
N = 0.01 s**-1 (constant with height)
Θ = 270 K (at the surface)
P = 1013.25 hPa (at the surface)
RH=0%

Topography: Witch of Agnesi ridge
1000 m height, 20000 m half width at half maximum
Ridge is located at the center of the domain.

Please find attached:

• sounding
• namelist.input
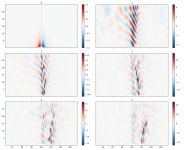
• expected_analytical_solution.png - the solution that would be expected from linear mountain wave theory. (first attached plot)
• perturbed_w_field.png - showing the w-field of an "unstable" solution in units m/s. (second attached plot)

WRF version used:

commit d154456d9ca813b487872b7d685f6cc1da455e82
Merge: dd5c4c3 93e197c
Author: Ming Chen <chenming@ucar.edu>
Date:   Mon Jun 3 17:18:32 2019 -0600

    Finalize WRFV4.1.1 by merging bug fixes from release-v4.1.1 branch onto master.

 

[kwerner]

Hi,
I consulted with our physics specialist here. He is unsure what is causing this, but did say that using a 1000 m hill is not going to give the analytic solution. Unfortunately in order to get a steady state, you would need to use 100 m or a smaller hill.

 

[johanneshorak]

Hi and thanks for the reply!

Sorry I did not mention this, I am aware that this won't match the analytical solution exactly, although I'd expect it to at least approximate it. That's what I wanted to use the pressure perturbation for(see the second thread) - from it you can calculate the drag coefficient and this can then be used as a measure of how close to the analytical solution the simulation actually is.

I've been thinking that reflections at the dampening layer or somewhere else in the domain might cause these artifacts, but I seem unable to get rid of them. So, unfortunately, I am still in need of help.

Apart from that - a steady state should develop for this sounding and topography at some point anyways shouldn't it? Even if there are non-linearities present.

 

[kwerner]

Hi,
I apologize for the delay in response. Our entire team was out of the country over the past couple of weeks, teaching a WRF tutorial in Europe.

The problem is likely that hills higher than a critical inverse Froude number will have wave breaking and will, therefore, have noisy non-steady solutions. Theoretically Nh/u < 0.85 for non-breaking waves. This would be exceeded for 1 km hills with typical u=10 m/s and N=0.01.

 

[johanneshorak]

Hi,
I apologize for the delay in response. Our entire team was out of the country over the past couple of weeks, teaching a WRF tutorial in Europe.

The problem is likely that hills higher than a critical inverse Froude number will have wave breaking and will, therefore, have noisy non-steady solutions. Theoretically Nh/u < 0.85 for non-breaking waves. This would be exceeded for 1 km hills with typical u=10 m/s and N=0.01.

No problem, I appreciate the reply. We finally found a working combination of model top height (26km), dampening layer thickness (16km) and dampening coefficient (0.3). The solution shows deviations from the one predicted by linear theory (e.g. stronger up/downdrafts) but is far from unrecognizable, even with the naked eye before looking into things like pressure drag and vertical momentum flux. Thanks for the help nonetheless!