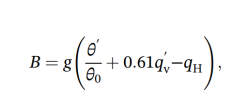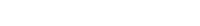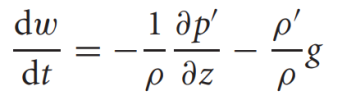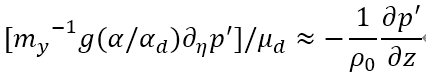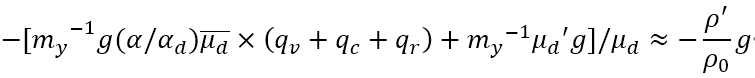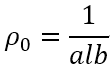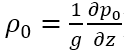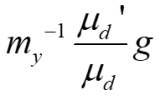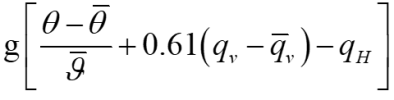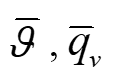Lanzhi Tang
New member
we used the WRF output ((w, u, v, P, AL, and ALB) to calculate the vertical velocity equation and found that it was not conserved. Then we further output the buoyancy in subroutine pg_buoy_w of module_big_step_utilities_em.F, and compared the perturbed pressure gradient force, buoyancy and other terms from WRF model and using WRF output data. we found that the result we calculated was similar to the WRF model except for buoyancy, which is almost an order of magnitude larger than WRF model. We wonder why the buoyancy is so different between calculation and WRF model. Beside, we find 1/ ALB is always larger than RHO, is that reasonable?
vertical speed equation: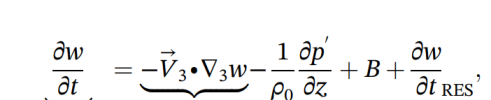
buoyancy calculation: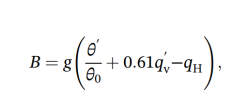
vertical speed equation:
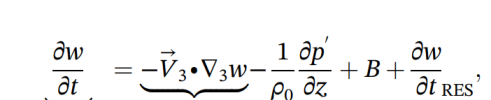
buoyancy calculation: