Upper limit recommendation for the grid spacing of the coarsest domain

[hconel]

In the best practices guide for WPS (link), it states that "It's best to keep the ratio of input data resolution to the coarsest grid resolution (on your domain) to no more than 1:10". So, my questions are:

1. This imposes a lower limit for the grid spacing of the coarsest domain, in other words, 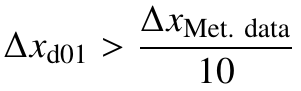. Is that correct? Sorry if the question sounds silly, but 1:10 being less than 1 makes the 'more than' wording confusing to me. Because if the implication is literally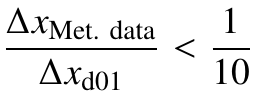, this means that for 80 km input resolution, coarsest grid resolution should be minimum 800 km, which is not what I see in the research papers (also the example in the link contradicts, where this ratio is 2.96).
2. If so, is there a recommended upper limit for the grid spacing of the coarsest domain?

 

[kwerner]

Hi,
The wording on that page is probably written poorly. I will take a look and make some modifications - especially because 10:1 is a bit more of a ratio (or difference) than it should be. We actually don't recommend the input data to be more of a difference than about 5:1 (where the input data is 5x the resolution of domain 1). Does that make sense?

 

[hconel]

Dear kwerner,
Thanks for the answer.
"5x the resolution" is vague for me, I can't be sure if it means a coarser or finer resolution.
What I understand is this: d01 (the outermost coarsest domain) can't be too fine, it should be coarse enough to satisfy

. So if the meteorological input grid spacing is 50km,

should be minimum 10km; it can be 20km, but it can't be 5km. Is that correct?

Again, I'm sorry for the hassle. Maybe this is because I'm not a native English speaker (and also lack of my technical WRF knowledge of course). I guess some mathematical description would work best.
Regards

 

[kwerner]

Hi,
I understand and no worries!

What I understand is this: d01 (the outermost coarsest domain) can't be too fine, it should be coarse enough to satisfy

. So if the meteorological input grid spacing is 50km,

should be minimum 10km; it can be 20km, but it can't be 5km. Is that correct?

You are absolutely correct. The higher the number, the more coarse the resolution. The lower the number, the higher the resolution. You can think of it like this: If you had a domain that covered the entire continent of Africa, and you split that domain into squares of 30 km in each direction, those squares would be relatively large and you would have much fewer of them than if you split the entire domain into squares that were 3 km each. You would have many more squares to cover the entire domain. And since WRF calculates on each grid point (or square), the solution would likely be much better with 3km resolution, than with 5 km. Does that make sense?

 

[hconel]

Hi,
I understand and no worries!

You are absolutely correct. The higher the number, the more coarse the resolution. The lower the number, the higher the resolution. You can think of it like this: If you had a domain that covered the entire continent of Africa, and you split that domain into squares of 30 km in each direction, those squares would be relatively large and you would have much fewer of them than if you split the entire domain into squares that were 3 km each. You would have many more squares to cover the entire domain. And since WRF calculates on each grid point (or square), the solution would likely be much better with 3km resolution, than with 5 km. Does that make sense?

Yes, thanks for taking the time to explain. I understand how nesting and grid spacing works, but that wording in the first post confused me. Now it's OK
So, this brings us to my main question in the title. How coarse can the outermost domain be? Is there some point after which increasing the grid spacing of d01 affects the solution quality and/or interaction with the input meteorological data negatively? For example, something like

?

 

[kwerner]

I'm not sure if anyone has tested the upper limit of coarseness for the outer domain. Your outer domain should not be more coarse than the resolution of your input data, and actually should probably be 3x or 5x higher resolution than the input data.

 

[hconel]

Thanks for the valuable information.
Regards