Hi,
I'm not sure I fully understand your question. When you say the run is simulating about the same number of days with 25% less processors, what do you mean by that? Do you mean it's simulating the same number of days in the same amount of time (real time), as if you had used 25% more processors? Are you satisfied with the results, or do you see them as being problematic? What do you mean by "do you think that this is the result of not spending as much time calculating the halo regions?" The reason you cannot use too many processors is that at some point the grid will be divided in a way that the halo regions are the majority of each grid cell, and there is no space in each grid cell left for calculating physical processes.
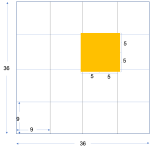
As for the question you asked in the email from Sept 4, if you uncomment the print statements in the python script and run it, you can see the full break-down. This script is meant to only calculate, based on the number of processors you want to use per node. Since you have 20 processors per node, if you have a domain size of 180x180, and you use 180 processors, the closest two factors of 180 are 12 and 15, meaning the processor break down will be:
180/12 = 15
180/15 = 12
As the minimum number of grid spaces allowed in each direction is 10, 180 processors is okay.
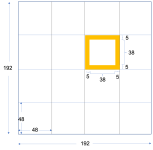
If, however, you tried to use 200 processors (which is adding 1 additional node with 20 processors), the breakdown would look like:
closest two factors: 10 and 20
180/10 = 18
180/20 = 9
While the east-west direction is okay, the number for north-south is 9, which is less than the minimum of 10. In this case, you should get an error telling you to use more processors.
If your domain is size 200x200, then the decomposition becomes different (meaning the closest factor pair allows many more processors):
Using 400 processors: closest two factors are 20 and 20
200/20 = 10
200/20 = 10
which falls within the limit, and is okay. A domain of size 1 grid cell less would not meet this requirement.
*
Note: I've once again modified the script for finding the correct number of processors. I realized I did not account for a case in which you could not use more than a single node. This does not apply for you, but if you want the updated version, please find it here.